Уравнение Бернулли

Уравнение Бернулли в первую очередь, уравнение дифференциальное первого порядка. Выглядит как :

в нем Q и P не прерывающаяся данная функция исходящая из Х.
а - неизменное число. Если ввести новую функцию z = у -0+1, то уравнение Бернулли придет к аналогичному линейному уравнению. Выведен данное вычисление в 1695 году.

Во вторую очередь является основой в уравнениях гидродинамики, она связывает (уже в готовой движущейся жидкости): V скорость + Р давление + h высота минимальной величины жидкости к участку отсчета. Данный метод был выведен в 1738 году, применяется для не горящим жидкостям имеющие постоянную плотность Р и которые находятся исключительно под силой тяжести. Выглядит данное уравнение как:

в нем g есть ускорение. При умножении данного уравнения на p, первый член выступит в качестве кинетической энергии в единице количества жидкости, другие два члена - в качестве потенциальной энергии. частично обусловленной с одной стороны как сила тяжести (крайнее значение) и давление с другой стороны. В этом виде и выходит закон о сохранении энергии. Во время когда по струе жидкости одна энергия к примеру кинетическая, возрастает, в это же время также падает потенциальная. Так когда поток в трубопроводе сужается, а его скорость возрастает (потому что за одинаковое время как через большое так и через маленькое сечение протекает одинаковый объем жидкости) и падает давление.

В уравнении Бернулли есть несколько важных моментов:

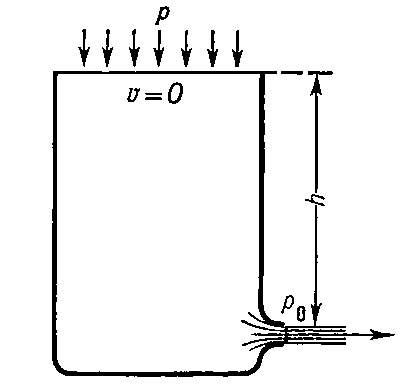
- Когда под силой тяжести из не закрытой емкости вытекает жидкость (изображено на первом рисунке)

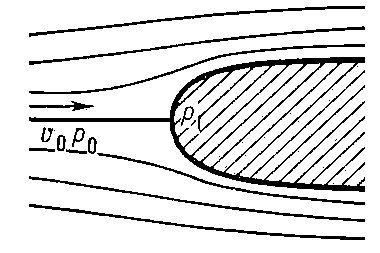
-Когда в спокойном потоке со скоростью V0 и давлением р0, встречается на пути проблема или препятствие, как изображено на втором рисунке, то жидкость по действием давления подпирает данное препятствие и как следствие замедляется сам поток; что интересно в подпоре, во время давления потока жидкости, в самом центре (назовем его - критическая точка) скорость равна 0. Вывод давление на критическую точку р₁=р₀+рV²₀/2. Присоединяем давление к ней, которое равно р₁ + р₀ = рv²₀/2, является динамическое давление либо напор скорости. Струя любой жидкости в потоке не сохраняет механическую энергию, расходует ее на силы трения и рассеивает на тепло. Нужно брать во внимание потери сопротивления, при использовании уравнения Бернулли в реальной жидкости.

Если ты молод и ищешь дополнительный заработок, но не знаешь где. Перейди по ссылке, заработок в интернете для подростка (http://odostatke.ru/zarabotat-podrostok.html) , там все подробно написано.