 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Определитель матрицы
Для решения заданий в высшей математике периодически нужно находить определитель матрицы. Встречается он не только в алгебре, но и в геометрии, математический анализ также может его содержать. Следовательно, нужно уметь находить определитель матрицы, так как это необходимо.
Что такое матрица - это таблица прямоугольной формы содержащая в себе различные выражения. Матрица может иметь n столбцов и m строк, ее называют как (m,n) - матрице.
Только квадратная матрица имеет определитель. Который больше всего встречается второго, третьего и четвертого порядка.
Следует запомнить что выражения (числа) стоят сами по себе, значит и вычитать ни чего не нужно, перестановку делать так же нельзя. Иногда можно поменять местами столбцы и строки парами. В результате это даст нам смену знака, но часто этого не требуется. Из чего следует, что в любом данном определителе, не нужно ни чего трогать или менять.
Разберемся в названиях обозначений:
- Определитель матрицы обозначается как {A}, реже встречается как D либо ?
Для того чтобы найти данное неизвестное число определителя нужно знать правила, алгоритмы и формулы. Такие как:
1) Для вычисления определителя второго порядка, нужна формула
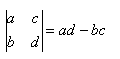
Разберем на примере:
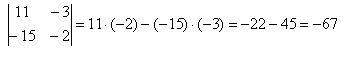
2) Для вычисления определителя третьего порядка, существует 8 способов, разберем 2 самых простых.
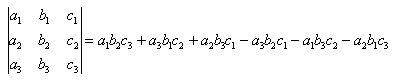
Разберем на примере:
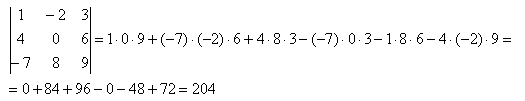
В использовании данной формулы, нужно быть внимательным что бы не допустить ошибку, так как формула довольно длинная. В избежание допущения ошибок существует еще один вариант решения. Названный как способ Саррюса. Он похож на предыдущий способ, но фишка заключается в том что через матрицу выражений проводятся параллельные линии, вынося за определитель в правую сторону два первых столбца.
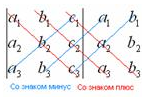
Таким образом числа зачеркнутые красным цветом вписываются с положительным знаком, а числа зачеркнутые синим цветом с отрицательным.
Разберем на примере:
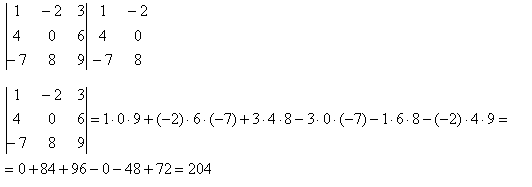
Если сравнить оба варианта вычисления, видно что они практически одинаковы, но во втором варианте допущение ошибки сводится к нулю, так как представлены множители.
Затронем еще один способ нормального вычисления, так как он используется в большинстве случаев. Найти определитель можно путем раскрытия его в любом столбце либо строке. Вычисляется путем сложения произведений выражений данного столбца или строки на алгебраические дополнения.
Для наглядности разберем определитель по первой строке.
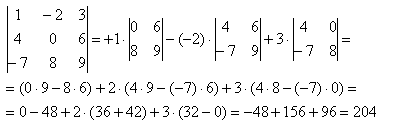
3) Для вычисления определителя четвертого порядка, нужно действовать так же как и при вычислении третьего порядка, просто таблица буде больше. Приведу пример и разложу на определитель третьего порядка, а потренироваться в решении вы сможете сами. В ответе должно получиться 18.
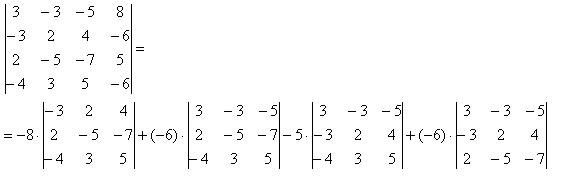
Это очень познавательно и интересно, главное быть внимательнее!
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!