 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Решение нелинейных уравнений
Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).
Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.
Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.
Рассмотрим несколько методов уточнения корней с определенно заданной точностью.
Методы численного решения нелинейных уравнений
Метод половинного деления.
Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)<0 не выполняется. Оставшаяся часть является новым отрезком, и деление пополам продолжается до тех пор, пока оставшийся отрезок не будет сравним с заданным параметром точности e, т.е. (b-a)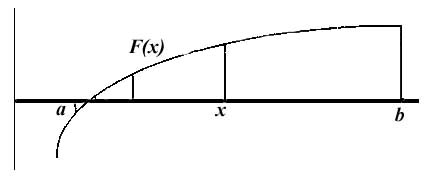
Рис.1. Использование метода половинного деления при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e<0,001 на отрезке [-1,0]. Обозначим начальную и конечную точки отрезка символами a и b соответственно.
В общем виде уравнение имеет вид: F(x)= х^3 – 0,2x^2 + 0,5x + 1,5
Разделим отрезок на 2 части: (a-b)/2 = (-1+0)/2=-0,5.
Если произведение F(a)*F(x)>0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.
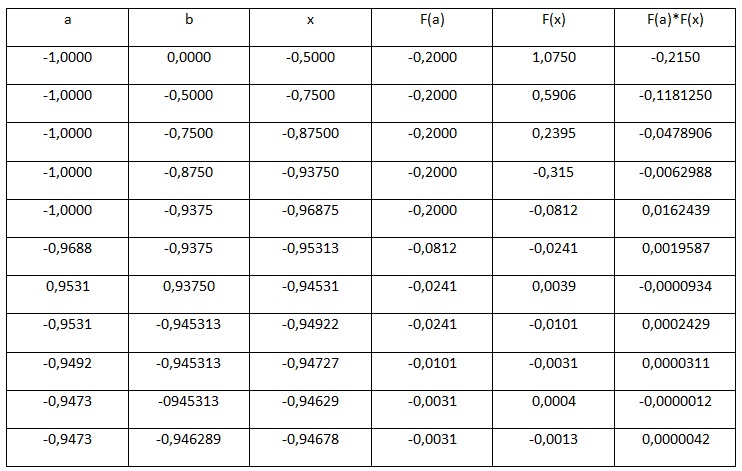
Рис.2. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Метод хорд.
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)<0, то правая часть отрезка переноситься в точку z (b=z), иначе переносится левая граница отрезка (а=z). Данное действие продолжается до достижения параметра точности e, т.е. F(z)< e.
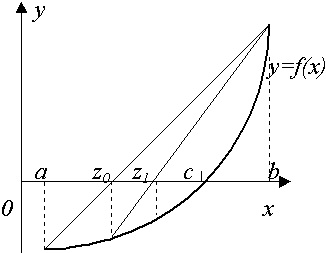
Рис.3. Использование метода хорд при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e<0,001 на отрезке [-1,0]. Обозначим начальную и конечную точки отрезка символами a и b соответственно.
В общем виде уравнение имеет вид: F(x)= х^3 – 0,2x^2 + 0,5x + 1,5
Найдем значения F(x) на концах отрезка [a,b]:
F(-1) = - 0,2>0;
F(0) = 1,5>0.
Определим вторую производную F’’(x) = 6x-0,4.
F’’(0)=-0,4<0.
На концах отрезка условие F(-1)F’’(-1)>0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:
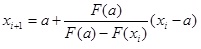
, где x0=b, F(a)=F(-1)=-0,2
Весь произведенный расчет отражен ниже в таблице.
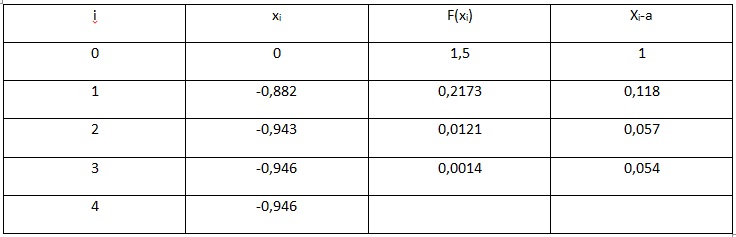
Рис.4. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Метод касательных (Ньютона)
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)
Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e<0,001 на отрезке [-1,0]. Обозначим начальную и конечную точки отрезка символами a и b соответственно.
В общем виде уравнение имеет вид: F(x)= х^3 – 0,2x^2 + 0,5x + 1,5
Определим первую и вторую производные: F’(x)=3x^2-0,4x+0,5, F’’(x)=6x-0,4;
F’’(-1)=-6-0,4=-6,4<0;
F’’(0)=-0,4<0.
Условие F(-1)F’’(-1)>0 выполняется, поэтому расчеты производим по формуле:
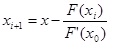
, где x0=b, F(a)=F(-1)=-0,2
Весь произведенный расчет отражен ниже в таблице.
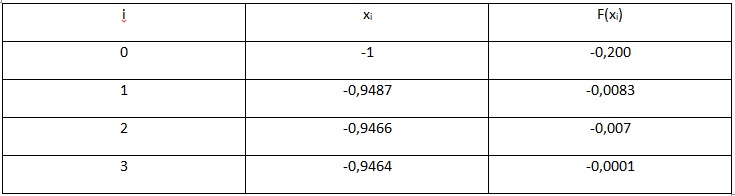
Рис.6. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
- Блог пользователя admin
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Я всегда ориентируюсь на это условие F(a)xF(b)<0, а так как при использовании метода половинного деления оно не выполняется, то и метод сам по себе я не использую. А в остальном спасибо, очень много полезного.