 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Простые формулы площади ромба!
В статье рассмотрим формулу площади ромба и не одну! На картинках покажем, как легко находиться площадь ромба по простым формулам.
Существует большое количество заданий на нахождение той или иной величины в ромбе и в этом нам помогут формулы, о которых и пойдет речь.
Ромб относится к отдельному виду четырехугольников, так как у него все стороны равны. Так же представляет частный случай параллелограмма в котором стороны АВ=ВС=СD=АD равны.
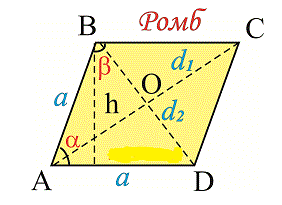
Заметка: Если Вам нужна курсовая, контрольная или дипломная работа, тогда вам на webmath.ru. или просто перейдите по ссылке заказать курсовую работу (http://www.webmath.ru/zakaz_kursovye.php).
Ромб обладает следующими свойствами:
- у ромба параллельные углы равные,
- сложение двух соседних углов равно 180 градусам,
- Пересечение диагоналей под углом в 90 градусов,
- Биссектрисами ромба, приходятся его же диагонали,
- Диагональ при пересечении делится на равные части.
Ромб обладает следующими признаками:
- Если у параллелограмма в котором диагонали встречаются под углом 90 градусов, то он называется ромбом.
- Если у параллелограмма равные стороны - это ромб.
- Если у четырехугольника равные стороны - это ромб.
- Если у четырехугольника в котором биссектриса это диагональ и диагонали встречаются под углом 90 градусов, то это ромб.
- Если у параллелограмма одинаковые высоты - это ромб.
Из вышеперечисленных признаков можно сделать вывод, что они нужны для того чтобы научиться отделять ромб от других схожих с ним фигур.
Так как в ромбе все стороны одинаковы периметр находится по следующей формуле:
Площадь ромба формула
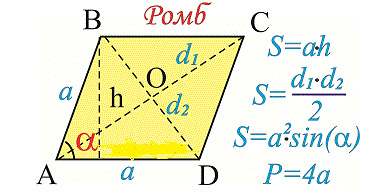
Данных формул несколько. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.
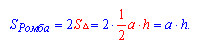
С помощью второй формулы можно решать задачи с известными диагоналями ромба. В этом случае площадью ромба будет: сумма диагоналей деленная на два.
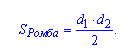
Очень просто в решении и не забудется.
Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла. При чем нет разницы какой угол. так как синус угла имеет единое значение.
Важно помнить что измерение площади происходит в квадратах, а периметра в единицах. Данные формулы очень легко применяются на практике.
Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности.
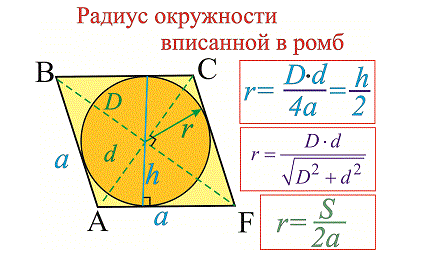
Для этого так же существует несколько формул:
В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. либо равняется половине высоты ( r=h/2).
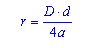
Во второй формуле взят принцип из первой, применяется мы знаем диагонали и стороны ромба.
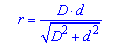
В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения.
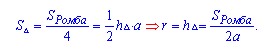
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!
Заметил, что для самые сложные формулы это с вписанной окружностью. Почему то тяжело запоминаются. Не подскажете, нет случайно какой - нибудь уловки чтобы эти формулы быстрее в голове сохранялись? Ну как таблица умножения на девять при загибании пальцев.
Вот когда задачи на нахождение площади ромба с рисунками идут еще проще как то, а когда самостоятельно еще и начертить нужно или еще хуже вообще без рисунка решать - темный лес начинается((((((((((((
По собственному плачевному опыту могу сказать, что свойства ромба нужно выучить на зубок, иначе потом сложно доказывать решение. Знать знаешь, а как доказать не знаешь.
До этой статьи я только одну площадь ромба знал, а оказывается их целых три в природе существует. Обязательно допишу себе в блокнотик, поступать то все равно на физ-мат.