Площадь равнобедренного треугольника формула

В данной статье речь пойдет о том как найти площадь равнобедренного треугольника и формулы для решения.
Равнобедренный треугольник это такой треугольник у которого две параллельные основанию стороны равны. Он изображен на рисунке.

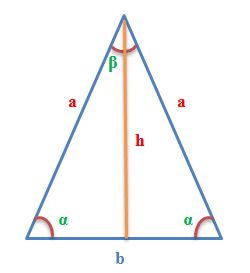
Стоит заметить что буквы которыми обозначены стороны и углы, используются в формулах, для вашего удобства.

Заметка: Если вам нужна качественно выполненная курсовая или контрольная работа, без посредников. Тогда Вам на сайт tvoi5.ru. Так же Вы можете перейти по ссылке курсовая на заказ (http://tvoi5.ru/zakazat-kursovuyu-rabotu.html) и все подробности.

Площадь равнобедренного треугольника формула.

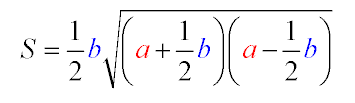
Первая формула говорит о том что площадь находится, если нам известна только одна сторона и основа треугольника. Получили эту формула с помощью использования общей формулы. Когда основным является формула Герона и стороны фигуры равны, она сама по себе будет выглядеть проще.

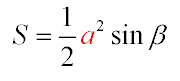
Во второй формуле говориться о том что площадь находится через боковые стороны и угол находящийся между ними. Или sin угла находящийся между боковых сторон, умноженный на половину квадрата одной из боковых сторон. Когда проводим высоту на боковой стороне её длина равняется а*sin?. Так как длину стороны мы знаем, то и её высота нам известна. Соответственно, площадь равнобедренного треугольника будет половина от их выражения. Если быть точнее. то целая величина делает площадь треугольника. Разделяя высотой прямоугольник, получаем два не больших прямоугольных треугольника. Диагональю будет сторона треугольника, в свою очередь она делит фигуру на две равные части. Из чего следует что искомая нами величина находится как половина величины одной стороны умножаемая на высоту.

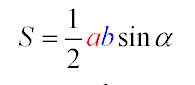
В третьей формуле площадь находится с помощью одной параллельной стороны, основания и угла находящегося на вершине. Другими словами можно сказать так: когда известен хоть один угол в равнобедренном треугольнике, с его помощью можно узнать и два других. Данная формула схожа со второй формулой, можно использовать и запомнить любую из них. Но из этой формулы выйдет пятая, которую опишу чуть ниже.

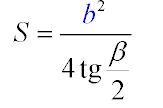
Четвертая формула показывает что найти площадь можно зная величину основания и угла при нем. Все углы у основания одинаковы и квадрат стороны основания разделенный на 4 tg пол угла, появившиеся от его боковых сторон. Когда внимательно разглядеть, можно понять, пол стороны основания b/2, при умножении tg (? /2) дает высоту. Которая в свою очередь играет роль медианы и биссектрисы, а значит tg (? /2)= (b/2)/h, из чего h=b/(2tg (? /2)) и сводиться к упрощенной формуле №5.

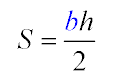
Итак пятая формула она гласит о том , что найти площадь можно с помощью высоты которая берет начало в вершине треугольника и заканчивается в его основании, при этом разделяя его на прямоугольные треугольники. А дальше как в третьей и четвертой формулах. Пол величины высоты умноженное на величину основания.

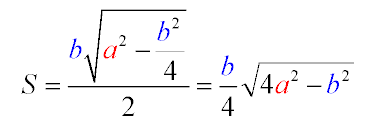
Шестая и заключительная формула. Она появляется в ходе решения площади треугольника через теорему Пифагора. Нам понадобиться высота, найденная в прошлой формуле. Она так же приходится катетом от прямоугольного треугольника, получившегося от боковой стороны, половины основания плюс высота. Гипотенузой будет боковая сторона, из квадрата гипотенузы (а) отнимем второй катет в квадрате. Так как он равняется полу - основания (b/2) значит квадрат = b2/4. Извлекая корень из полученного , найдем высоту.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---