 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Формула Эйлера
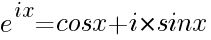
Формула Эйлера показывает, как связаны между собой экспоненциальная функция eix и тригонометрические функции синуса и косинуса аргумента x.
- , где i - мнимая единица.
- Если заменить x на -x, получим ещё один вариант формулы Эйлера:
- Рассмотрим один из примеров использования формулы Эйлера.
- Возведём в квадрат обе части уравнения
- Если учесть, что
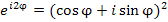 .получается, что
.получается, что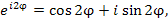 Известно, что если два комплексных числа равны, то равны их действительные и мнимые части. Тогда,
Известно, что если два комплексных числа равны, то равны их действительные и мнимые части. Тогда,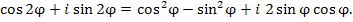
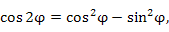
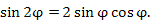


 Образовательный портал
Образовательный портал
 Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!