 Онлайн калькулятор
Онлайн калькулятор
 Решение матриц
Решение матриц
 Конвертор величин
Конвертор величин
 Решение кв. уравн.
Решение кв. уравн.
 Таблица Брадиса
Таблица Брадиса
 Тригоном. таблицы
Тригоном. таблицы
 Тесты и игры
Тесты и игры
 Решить задачу
Решить задачу
 Таблица производных
Таблица производных
 Калькулятор дробей
Калькулятор дробей
 Фонетический разбор
Фонетический разбор
 Редактор формул
Редактор формул
Котельников теорема
В.А. Котельников теорема, доказанная им в 1933 году, которая стала основополагающим положением в радиотехники. Она дает возможность для точного восстановления сигнала с небольшим радиусом, отталкиваясь от отсчетных данных, которые были взяты в одинаковых промежутках времени.
Как строится ортонормированный базис, рассмотрим. Ортогональный сигнал состоит из двух сигналов с небольшим радиусом действия. Которые относятся к семейству:
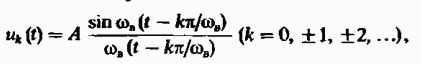
Можно сделать так чтобы, сигнал получился единичным с помощью подходящего амплитудного множителя А. Получим ортонормированный базис, который может разделить произвольный сигнал с небольшим радиусом в обобщенный ряд Фурье.Посмотрим на функцию
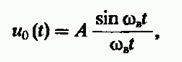
исходя из того, что нормой для сигнала uk одинаковая и не зависит от сдвигов время. Потому что
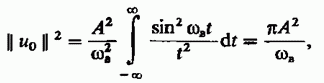
uk станут ортонормированными, когда
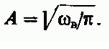
постоянной продолжительности функций
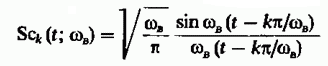
образующей базис Котельникова в линейной плоскости низких по частоте сигналов с радиусами, сверху ограниченные ?в . Отдельно стоящая функция Sck (t; ?в) - является k-отсчетной.
Формулировка теоремы Котельникова состоит из того, что произвольный сигнал, в радиусе которого нет частоты больше fв, Гц. Можно восстановить тогда, когда мы знаем отсчетные данные данного сигнала, которые были взяты в одинаковых промежутках времени 1/(2fв) с.
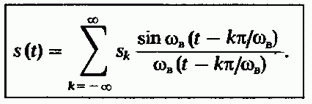
Рассмотрим на примере
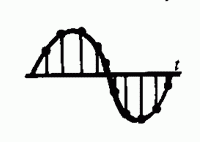 Получен сигнал s(t) = cos(?0t + ?0)
Получен сигнал s(t) = cos(?0t + ?0)
Взяв определенное количество времени между отсчетов t0, мы сможем восстановить какой-либо сигнал, если в его радиусе нет элементов состоящих на частоте, которая располагается дальше граничащей высоты ?в = ?/t0
Когда ?0 меньше ?в, значит мы можем применить данную теорему к нашему гармоническому сигналу Sk = cos(k ? ?0/ ?в + ?0)
НА один промежуток сигнала, нужно две выборки. Когда нарушается условие теоремы, то есть отсчет взят не так часто как нужно, восстановить сигнал не получится.
 В теореме Котельникова есть важный момент, заключается он в том, что она имеет конструктивный характер. Теорема Котельникова не только помогает в разделении сигналов в ряды, но так же ищет вариант для восстановления непрерывного сигнала, с помощью отсчетных данных.
В теореме Котельникова есть важный момент, заключается он в том, что она имеет конструктивный характер. Теорема Котельникова не только помогает в разделении сигналов в ряды, но так же ищет вариант для восстановления непрерывного сигнала, с помощью отсчетных данных.
Если есть несколько генераторов, отдающих на выходе отсчетные функции Sck = (t; ?в). Амплитуда сигналов генераторов идет в пропорции с отсчетными данными Sk, а сами они являются управляемыми. При объединении колебаний на выходе, отправив их в сумматор, мы получим на выходе их него сиюминутные данные сигнала.
Заметка: грузоперевозки по россии (http://transportkzn.ru/index.html) предоставляет компания "Транспорт Казань". Доступно и надежно, грузоперевозки россия.
- Блог пользователя kak-reshit
- Войдите на сайт для отправки комментариев


 Образовательный портал
Образовательный портал Reshit.ru может исчезнуть — нужна ваша поддержка!
Reshit.ru может исчезнуть — нужна ваша поддержка!